PEOPLERESEARCHGITHUB

Alpha Invariance: On Inverse Scaling Between Distance and Volume Density in Neural Radiance Fields

CVPR 2024

  1. Joshua Ahn*1
  2. Haochen Wang*2
  3. Raymond A. Yeh3
  4. Greg Shakhnarovich2
  1. University of Chicago 1
  2. TTI-Chicago 2
  3. Purdue University 3
  1. arxiv
  1. Alpha Invariance
  2. Current practices
  3. Two Common Failure Modes
  4. Our proposal
  5. GumbelCDF activation
  6. High transmittance initialization
  7. Acknowledgements
  8. Bibtex
Scale-ambiguity in 3D scene dimensions leads to magnitude-ambiguity of volumetric densities in neural radiance fields, i.e., the densities double when scene size is halved, and vice versa. We call this property alpha invariance. For NeRFs to better maintain alpha invariance, we recommend 1) parameterizing both distance and volume densities in log space, and 2) a discretization-agnostic initialization strategy to guarantee high ray transmittance. We revisit a few popular radiance field models and find that these systems use various heuristics to deal with issues arising from scene scaling. We test their behaviors and show our recipe to be more robust.
Fig 1: Python pseudocode for our 1) GumbelCDF density activation and 2) high transmittance initialization. It is numerically stable since log densities, log distances, and high transmittance offset naturally cancel out one another when scene size LL or the ray sampling strategy changes.

Alpha Invariance

NeRF performs volume rendering by alpha compositing. Alpha is primarily a discrete concept. It is the opacity of a local segment. In NeRF, however, each discrete alpha is a function of two continous variables: distance and volume density. Since physical reality does not change with respect to the unit of the measuring ruler, it is the case that distance and density vary inversely to compensate for each other.
The Blender synthetic dataset has a scene radius of 4.04.0 while Mip-NeRF 360's contraction operation confines unbounded scenes to within a sphere of radius 2.02.0. Ultimately, there is no "correct" scene size for 3D reconstruction, and the choice is often arbitrarily made by the practitioner. Fig. 2 contains visualizations of volume densities when the systems are trained at different scene sizes.
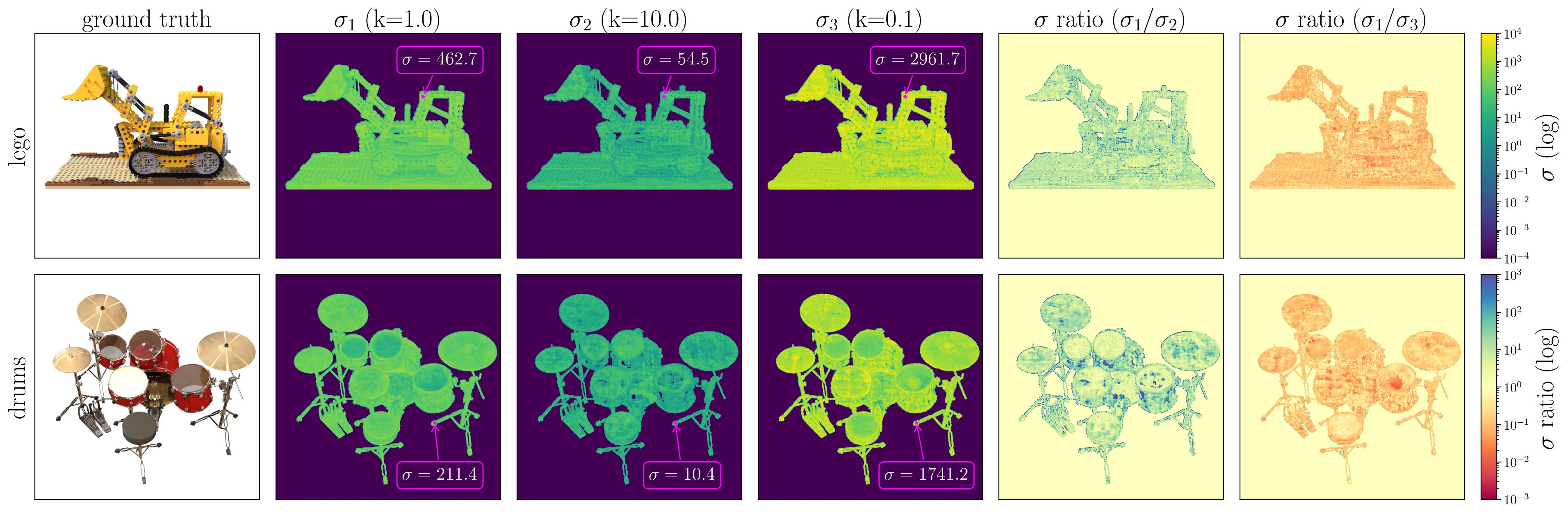
Fig 2: Surface σ\sigma statistics, extracted from vanilla NeRF trained on the lego and drums scenes from the Blender dataset and Nerfacto trained on the garden and bicycle scenes from the Mip-NeRF 360 dataset. Along each ray, the surface point is defined as the 50th percentile location of the volume rendering CDF. We annotate a few prominent points, and also produce two σ\sigma division images that show the overall ratio of the numerical range of σ\sigma at different scaling factors. The ratio of σ\sigma is empirically close to 1/k1/k.

Current practices

Vanilla MLP-NeRF parameterizes the volume density σ(x)\sigma(x) with a ReLU\mathtt{ReLU} activation. Mip-NeRF advocates for the use of softplus\mathtt{softplus} activation, out of concern that ReLU\mathtt{ReLU} might get stuck since there is no gradient if inputs are negative. DVGO uses a fixed local interval size (DVGO-7). TensoRF scales the local interval size by a constant (TRF-14). Plenoxels uses ReLU\mathtt{ReLU} with a very large learning rate on σ(x)\sigma(x) at the beginning of optimization before decaying it as convergence improves (PNXL-111). Instant-NGP uses exp\mathtt{exp} activation. The motivation is not discussed in the paper, but the author provides a comment on GitHub (INGP-D577). Some of these decisions have been adopted by more recent works. For example, HexPlane and LocalRF follow TensoRF's interval scaling strategy, while works building on top of Instant-NGP tend to use the truncated exp\mathtt{exp} activation for numerical stability.

Two Common Failure Modes

We observe two common failure modes when we train these systems with different scene sizes.
  • When the scene size is small, large densities are required at solid regions. Activations like softplus\mathtt{softplus} and relu\mathtt{relu} struggle at this task, especially for voxel NeRFs.
  • When the scene size is large, densities at initialization are often too large, resulting in an opaque, cloudy scene that traps optimization at bad local optima.

Our proposal

GumbelCDF activation

Since the magnitudes of both distance and volume density are scale-ambiguous, and their product determines the local alpha of a ray segment, we suggest to parameterize both in log space. Small interval sizes used under importance sampling strategies naturally cancel out the large density values needed to achieve a target alpha level, ensuring numerical stability. We plot how the activation functions relate to local alpha in Fig. 3 below.
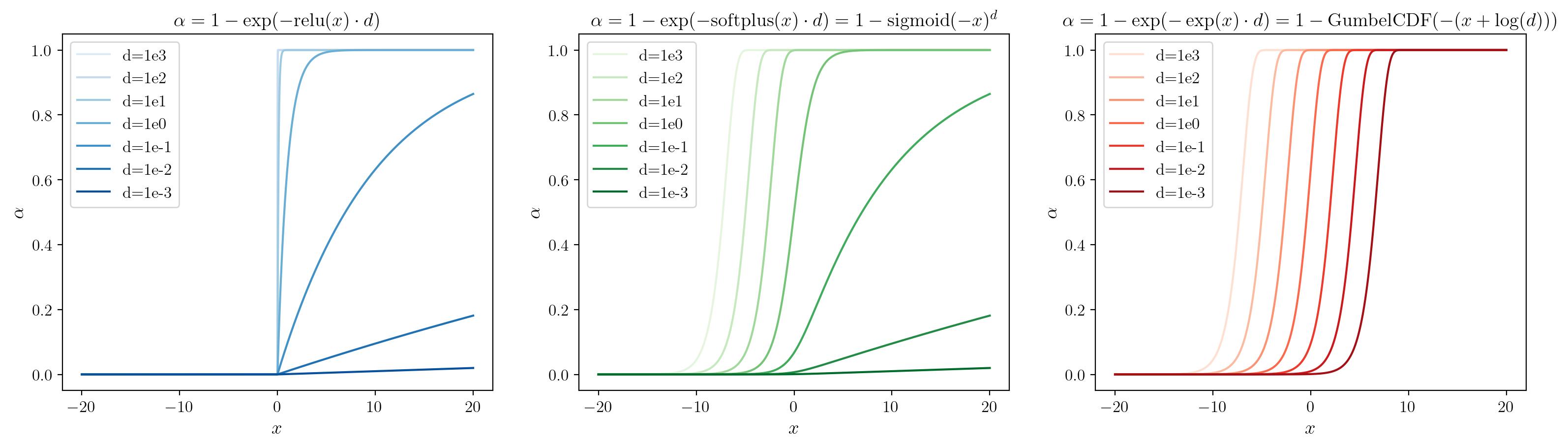
Fig 3: α\alpha as a function of the raw input xx and dd; here we focus on α\alpha as a function of xx, with different activation functions σ(x)\sigma(x), for a set of fixed values of interval lengths dd.

High transmittance initialization

In order to prevent the cloudiness trap, we want the scene to be transparent at initialization, i.e. every ray has high transmittance. Assuming the underlying neural field output is sampled from N(μ,τ2)\mathcal{N}(\mu, \tau^2), and given a transmittance target T′T' of say, 99%99\%, we can write down a closed-form expression for a density offset that in expectation guarantees a ray of length LL to have the desired transmittance level:
μ=log⁡log⁡1T′−log⁡L−τ22.\begin{align} \mu = \log \log \frac{1}{T'} - \log L - \frac{\tau^2}{2}. \end{align}
Merging the offset with the GumbelCDF activation produces the following expression for local alpha as a function of interval size dd and neural field output xx:
α=1−exp⁡(−exp⁡(x+log⁡d+μ))=1−exp⁡(−exp⁡(x+log⁡dL+log⁡log⁡1T′−τ22)),\begin{align} \alpha &= 1 - \exp(-\exp(x + \log d + \mu) ) \nonumber \\ &= 1 - \exp \left( -\exp(x + \log \frac{d}{L} + \log \log \frac{1}{T'} - \frac{\tau^2}{2}) \right), \end{align}
where log⁡dL\log{\frac{d}{L}} is invariant w.r.t. scene scaling. One interpretation is that we are working with distance ratios and are thus effectively hardcoding the overall scene size to 1.01.0. But this is only possible with the extra offset terms, without which, assuming τ=1.0, T′=0.99\tau=1.0,~ T'=0.99, the scene size LL would need to be set to 0.0060.006 in order to meet the high transmittance target. See Fig. 4 for ablations on the necessity of high transmittance offset on the TensoRF architecture, and Fig. 5 for visuals from the Nerfacto architecture.
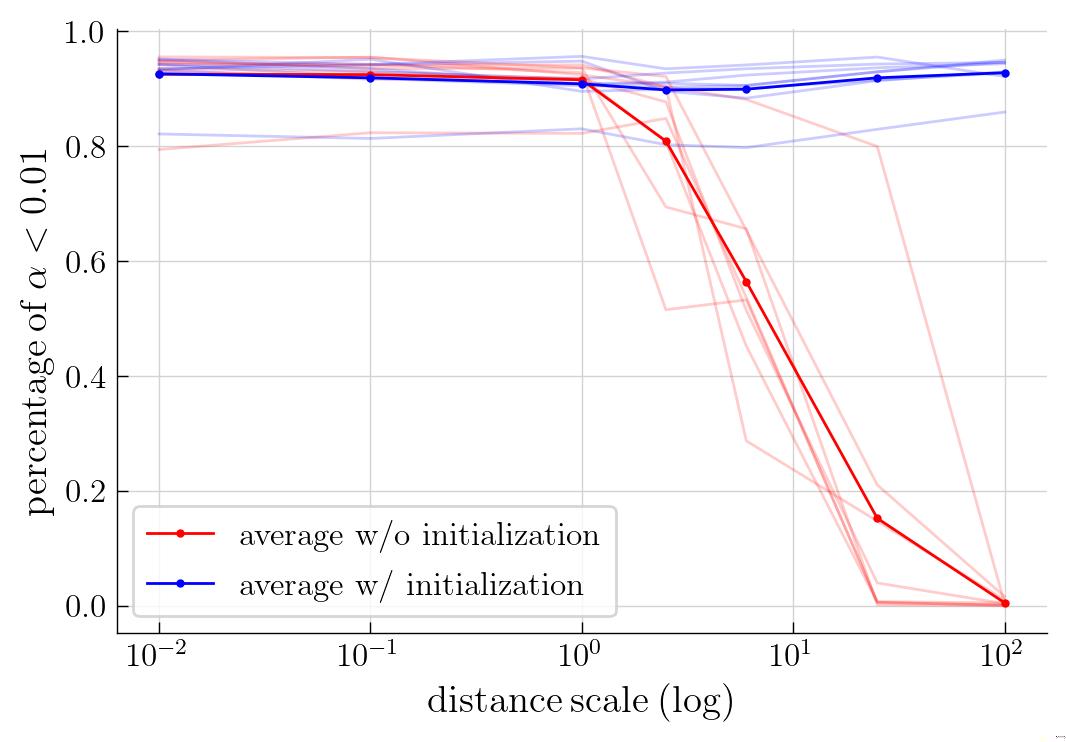
Fig 4: The amount of empty space in a trained NeRF, with distance scaling kk ranging from 10−210^{-2} to 10210^{2}. The model is TensoRF using an exp⁡\exp parametrization on σ\sigma. We query a dense uniform grid of samples and consider a location to be empty if the local alpha is below 0.010.01. Each faint line corresponds to a scene from the blender dataset; the solid line is the dataset average. With our high transmittance initialization, we prevent over-densification even when kk is large.
Fig 5: RGB-image and depth-maps produced from Nerfacto on the ballroom, auditorium, and courtroom scenes from Tanks and Temples at a large scene scaling k=25k=25. Not using our high transmittance initialization strategy causes the optimization to get stuck with cloudy floaters.

Acknowledgements

We thank members of PALS, 3DL, and Michael Maire's lab for advice on the manuscript. This work was supported in part by the TRI University 2.0 program. JA is supported by UChicago's Quad Research Fellowship and the Dingwall Fdn. Korean Ancestry Grant.

Bibtex

@article{alphainvariance2024,
  title={Alpha Invariance: On Inverse Scaling Between Distance and Volume Density in Neural Radiance Fields},
  author={Joshua Ahn and Haochen Wang and Raymond Yeh and Greg Shakhnarovich},
  journal={CVPR},
  year={2024},
}

Made with ❤  by Yours Truly. Design inspired by distill. Header layout by Saining Xie's group.