Score Jacobian Chaining: Lifting Pretrained 2D Diffusion Models for 3D Generation

CVPR 2023

1. arxiv
2. code
3. colab

1. Chain Rule on Score Function
2. Denoiser's Out of Distribution Problem
3. Perturb and Average Scoring (PAAS)
4. Generalizing $D$ to SDEdit Guidance
5. Relation to DreamFusion
6. Acknowledgements

A diffusion model learns to predict a vector field of gradients. We propose to apply chain rule on the learned gradients, and back-propagate the score of a diffusion model through the Jacobian of a differentiable renderer, which we instantiate to be a voxel radiance field. This setup aggregates 2D scores at multiple camera viewpoints into a 3D score, and repurposes a pretrained 2D model for 3D data generation. We identify a technical challenge of distribution mismatch that arises in this application, and propose a novel estimation mechanism to resolve it. We run our algorithm on several off-the-shelf diffusion image generative models, including the recently released Stable Diffusion trained on the large-scale LAION dataset.

Fig 1: Results for 3D generation using Score Jacobian Chaining with Stable Diffusion v1.5 as the pretrained model.

Chain Rule on Score Function

Starting from the assumption that the 3D asset parameter $\vtheta$ is as likely as its 2D renderings $\vx_\pi$, i.e. $\log q_\sigma(\vtheta) \propto \E_{\pi} \big[ \log p_\sigma(\vx_\pi) \big]$, we show the following relationship between 2D scores and the 3D score. Namely, a 3D score should be computed by the Vector-Jaocobian product of 2D score and renderer Jacobian over different camera viewpoints.

$$\begin{equation*} \underbrace{\grad_{\vtheta}\log q_\sigma(\vtheta)}_{\text{3D score}} = \E_{\pi} [ ~ \underbrace{\grad_{\vx_\pi}\log p_\sigma(\vx_\pi)}_{\text{2D score; pretrained}} \cdot \underbrace{ J_\pi \vphantom{\grad_{\vx_\pi}\log p(\vx_\pi)} }_{\text{renderer Jacobian}} ]. \end{equation*}$$

The arxiv manuscript uses $q_\sigma(\vtheta) \propto \E_{\pi} \big[ p_\sigma(\vx_\pi) \big]$ followed by Jensen's. The detour is not correct and not needed. We will update it in the next release. The form of the Vector-Jacobian product remains the same.

Denoiser's Out of Distribution Problem

To compute the 2D score $\grad_{\vx_\pi}\log p_\sigma(\vx_\pi)$, a first attempt is to invoke the formula

$$\begin{equation*} \text{score}(\vx_\pi, \sigma) \triangleq \frac{{D}(\vx_\pi, \sigma) - \vx_\pi}{\sigma^2}. \end{equation*}$$

However this leads to an out-of-distribution problem. During training, when conditioned at $\sigma$, the denoiser $D$ has only seen noisy input of the form $\vy + \sigma \vn$, where $\vy \sim p_{\text{data}}, \vn \sim \gauss{0}{\rmI}$. Note that $\vy + \sigma \vn$ is not just noisy, it is also numerically large. Whereas a rendered RGB image $\vx_\pi$ from a 3D scene is capped within $[-1, 1]$, $\vy + \sigma \vn$ has variance $1 + \sigma^2$ with large numerical range. We illustrate the OOD problem in the figure below.

Fig 2: Illustration of denoiser's OOD issue using a denoiser pretrained on FFHQ. When directly evaluating $D(\vx_{\text{blob}}, \sigma=6.5)$ the model did not correct for the orange blob into a face image. Contrarily, evaluating the denoiser on noised input $D(\vx_{\text{blob}} + \sigma \vn, \sigma)$ produces an image that successfully merges the blob with the face manifold. Note that this figure looks very much like SDEdit.

Perturb and Average Scoring (PAAS)

To resolve the OOD issue, we propose Perturb and Average Scoring (PAAS). It computes score on a non-noisy image $\vx_\pi$ by perturbing it with noise, and averaging the score computed on each of perturbations.

$$\begin{align*} &\nescore{}(\vx_\pi, \sqrt{2}\sigma) \\ \triangleq & \E_{\vn \sim \gauss{0}{\rmI}}~ \left[\mathrm{score}(\vx_\pi + \sigma\vn, \sigma)\right] \\ =& \E_{\vn}~ \left[\frac{{D}(\vx_\pi + \sigma\vn, \sigma) - (\vx_\pi + \sigma\vn)}{\sigma^2}\right] \\ =& \E_{\vn}~ \left[ \frac{{D}(\vx_\pi + \sigma\vn, \sigma) - \vx_\pi}{\sigma^2} \right] \bcancel{ - \underbrace{\E_{\vn}\left[\frac{\vn}{\sigma}\right]}_{\text{=$0$}} } \end{align*}$$

We show that mathematically, PAAS approximates the score on non-noisy input $\vx_\pi$ at an inflated noise level of $\sqrt{2}\sigma$, and we illustrate its intuition in the figure below.

$$\begin{equation*} \nescore{}(\vx_\pi, \sqrt{2}\sigma) \approx \score{\vx_\pi}{\sqrt{2}\sigma}. \end{equation*}$$

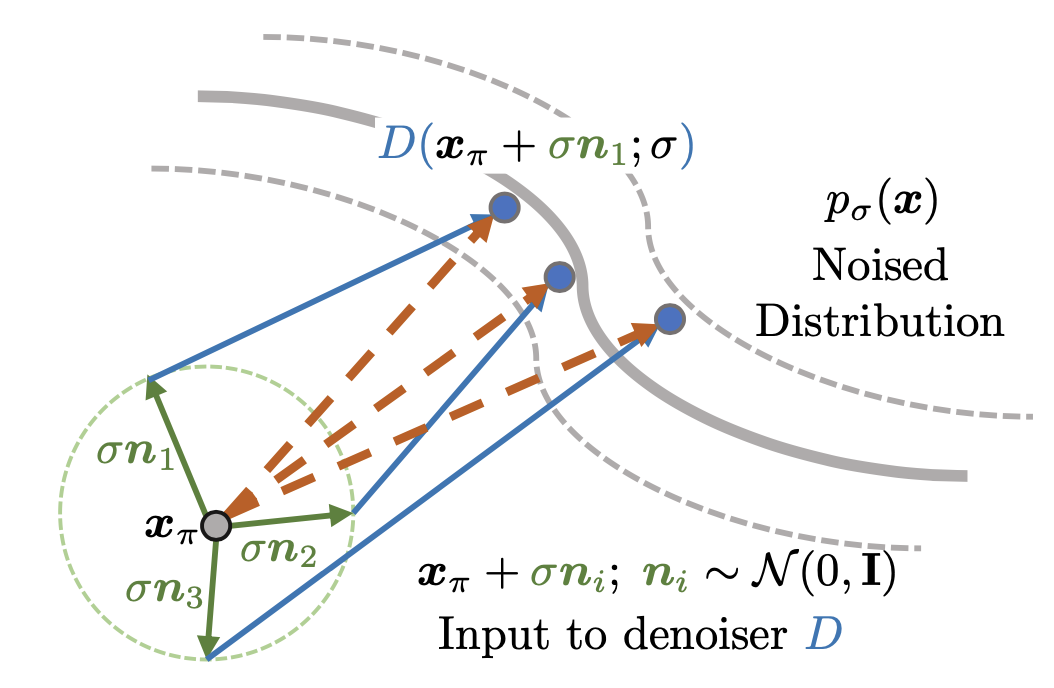
Fig 3: Computing PAAS on 2D renderings $\vx_\pi$. Directly evaluating $D(\vx_\pi; \sigma)$ leads to an OOD problem. Instead, we add noise to $\vx_\pi$, and evaluate $D(\vx_\pi + \sigma \vn; \sigma)$ $\textcolor{blue}{\textbf{blue}}$ dots. PAAS is then computed by averaging over the $\textcolor{brown}{\textbf{brown}}$ arrows, corresponding to multiple samples of $\vn$.

Generalizing $D$ to SDEdit Guidance

A nice benefit of writing the PAAS gradient as ${D}(\vx_\pi + \sigma\vn, \sigma) - \vx_\pi$ is that it shows this gradient is merely the $l2$ loss gradient of current iterate $\vx_\pi$ and 1-step inference ${D}(\vx_\pi + \sigma\vn, \sigma)$. If we use a full inference pipeline, then it becomes multiview SDEdit guidance i.e. $\text{SDEdit}(\vx_\pi, \sigma) - \vx_\pi$. It was proposed by SparseFusion, and they call it multi-step denoising.

Relation to DreamFusion

Our formulation including Lemma 1 and Claim 1 in the paper were done before DreamFusion was released on Sept. 29th, 2022. At the time, our team was working on the LSUN Bedroom model, an unconditioned diffusion model by Dhariwal and Nicol; we thought bedrooms contain the most interesting 3D structure and were beyond the capability of 3D GANs. It turns out that making PAAS work on an unconditioned diffusion model is very challenging, even on 2D, especially with the Bedroom model (see Fig 4. of the paper). DreamFusion shows that a language conditioned diffusion model could make use of language forcing (unusually high guidance scale) to make optimization easier by making the image distribution narrower. We are influenced by this insight. That being said, this approach has its drawbacks such as over-saturated colors and limited content diversity per language prompt, and at the moment it is unclear how to deal with diffusion models which are unconditioned.

Acknowledgements

The authors would like to thank David McAllester for feedbacks on an early pitch of the work, Shashank Srivastava and Madhur Tulsiani for discussing the $\sqrt{2}$ factor on synthetic experiments. We would like to thank friends at TRI and 3DL lab at UChicago for advice on the manuscript. This work was supported in part by the TRI University 2.0 program, and by the AFOSR MADlab Center of Excellence.